Databend Sort 优化

最近 Databend 针对数据排序进行了一波性能优化，在此记录一番。

排序操作在数据库中十分常见与重要。最常见的用法是将数据表按照某几个字段进行排序，或者找出数据表中最大或最小的几行（TopN）。

1
2

SELECT * FROM table ORDER BY co11, col2; -- normal sort
SELECT col FROM table ORDER BY col LIMIT n; -- top n

Databend 的 RECLUSTER TABLE 命令也与排序息息相关，此命令会将数据表按照 CLUSTER KEY 重新组织，并最终使得底层数据分部遵循 CLUSTER KEY 有序排列。

排序在数据库中的重要性不言而喻。在优化之前，Databend 的排序实现比较简单，性能表现不太理想，所以需要进行重新设计与优化。

历史实现

Databend 曾经的排序实现的十分简单——那就是不断地进行归并排序。

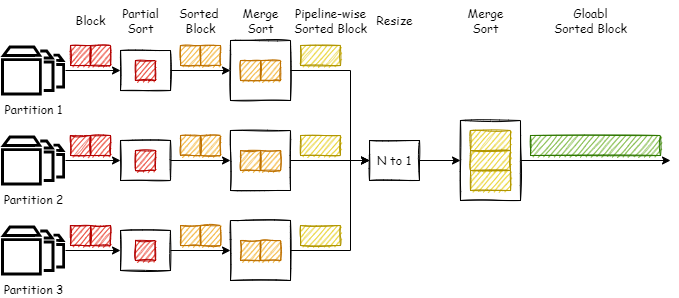
如图所示，Databend 会为每一个数据源分组建立一条 Partial Sort 流水线，然后通过 Resize 管道将多个流水线合一，然后再进行一次整体的归并排序得到最终的全序数据。

性能分析

很容易看出，这种流水线的瓶颈主要在于 MergeSort 阶段（火焰图也印证了这一点）。在实现中，MergeSort 会等待上游数据全部输入才会开始进行归并排序，因为只有这样才能保证数据最终的有序。然而，这种设计的一个最直接的影响就是：MergeSort 阻塞了流水线，下游算子需要等待所有数据块全部堆积在最后一个 MergeSort 并进行归并排序之后才能拿到数据。

1

SELECT AVG(col) FROM (SELECT col FROM table ORDER BY col LIMIT n);

设想这样一条 SQL，AVG(col) 需要整个 (SELECT col FROM table ORDER BY col LIMIT n) 执行完毕后才能开始计算，这显然效率是十分低下的。

题外话：为了缓解排序阻塞带来的影响，Databend 会将 LIMIT 下推到排序阶段，使得归并排序得到目标数量行之后便可以直接输出，这在一定程度上优化了 TopN 。

所以直观的看来，有两个优化方向：第一个是并行化归并排序（见最后一节），第二种是让 MergeSort “流起来“，目前的实现选择了后者。

优化一：流式 MergeSort

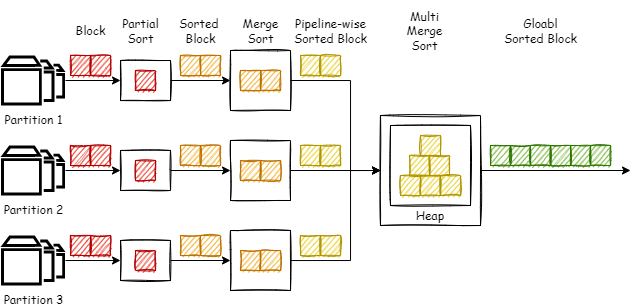
如图所示，这里主要的改造是将 Resize 和第二个 MergSort 合并为了一个 MultiMergeSort，而此次优化的重点便是这个 MultiMergeSort。这个算子的主要思想很显而易见，那就是使用堆来进行多路归并。以小根堆为例，若 N 路升序序列都至少有一个元素被 push 入了堆（按照顺序），此时堆顶元素则为全局最小元素。依据这个特性，我们可以在从上游拉取数据并向堆中 push 元素的同时，pop 出堆顶元素输出到下游，使数据”流动“起来，让下游算子不用等到整个序列排序完成后才能开始工作。

实现细节

DataBlock Cursor

排序是粒度是行，但是在向量化执行下，算子之间传递的数据自然不会是一行一行的数据，而是一个一个的数据块，一个数据块中包含有多行。所以这里需要引入一个新的数据结构 Cursor 来表示具体的某一行数据。

1
2
3
4
5
6

struct Cursor {
    pub input_index: usize,     // Cursor 指向的数据是来自于哪个 input port
    // pub block_index: usize,     // Cursor 指向的是哪一个 data block。可以省略，因为 heap 中每一个 block 只可能来自于不同的 input port。
    pub row_index: usize,         // Cursor 指向的是哪一行
    // other fields
}

我们每次只用将 Cursor 推入堆中即可。Cursor 间的比较即为对应行排序键之间的比较。

Heap 操作

针对堆的操作是整个 MultiMegeSort 的核心，整体算法流程大概为：

1. 若堆中元素不少于输入数，执行下一步；否则结束此流程。
2. 弹出堆顶 Cursor，将 Cursor 所指向的行推入待输出队列。
3. 将 Cursor 指向下一行，若已遍历 block 中所有行，则标记此 input 可以拉取下一个 block 数据；否则，将递增后的 Cursor 放回堆中。
4. 若待输出队列累计已达要求（limit 或 block_size），则退出此流程准备输出；否则，返回第 1 步。

对于上述第 2~3 步，有一个可以优化的地方，如下图所示。

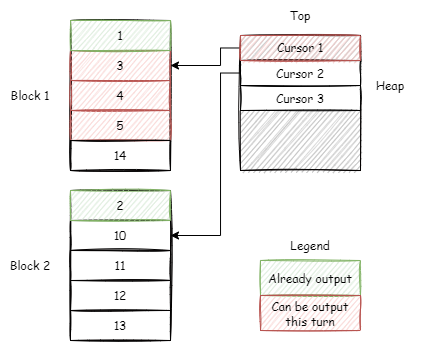
我们其实不用每次都将 Cursor 回堆，徒增一次 O(log(N)) 的操作。如果递增后的 Cursor 仍然比下一个堆顶元素小，那么我们可以继续将递增后的 Cursor 所指向的行放入输出队列。更加特殊的，如果当前 Cursor 所指向的 block 的最后一行元素都比下一个堆顶元素小，那么可以直接将从当前 Cursor 起此 block 中的所有数据都放入待输出队列。

通过实验证明，这个小细节会让查询快很多。对于一些比较特殊的语句甚至有 3 倍以上的提升，比如下面这个语句：

1
2

SELECT * FROM numbers(10000000) ORDER BY number;
SELECT * FROM numbers(10000000) ORDER BY number DESC;

因为 numbers 产生的 block 之间没有数据交叉，每个 block 之间本身就具有顺序。

这整体部分的代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

while self.heap.len() >= nums_active_inputs && !need_output {
    match self.heap.pop() {
        Some(Reverse(mut cursor)) => {
            let input_index = cursor.input_index;
            if self.heap.is_empty() {
                // If there is no other block in the heap, we can drain the whole block.
                need_output = self.drain_cursor(cursor);
            } else {
                let next_cursor = &self.heap.peek().unwrap().0;
                // If the last row of current block is smaller than the next cursor,
                // we can drain the whole block.
                if cursor.last().le(&next_cursor.current()) {
                    need_output = self.drain_cursor(cursor);
                } else {
                    let block_index = self.blocks[input_index].len() - 1;
                    while !cursor.is_finished() && cursor.le(next_cursor) {
                        // If the cursor is smaller than the next cursor, don't need to push the cursor back to the heap.
                        self.in_progess_rows.push((
                            input_index,
                            block_index,
                            cursor.advance(),
                        ));
                        if let Some(limit) = self.limit {
                            if self.in_progess_rows.len() == limit {
                                need_output = true;
                                break;
                            }
                        }
                    }
                    if !cursor.is_finished() {
                        self.heap.push(Reverse(cursor));
                    } else {
                        // We have read all rows of this block, need to read a new one.
                        self.cursor_finished[input_index] = true;
                    }
                }
            }
            // Reach the block size, need to output.
            if self.in_progess_rows.len() >= self.block_size {
                need_output = true;
                break;
            }
            if self.cursor_finished[input_index] && !self.input_finished[input_index] {
                // Correctness: if input is not finished, we need to pull more data,
                // or we can continue this loop.
                break;
            }
        }
        None => {
            // Special case: self.heap.len() == 0 && nums_active_inputs == 0.
            // `self.in_progress_rows` cannot be empty.
            // If reach here, it means that all inputs are finished but `self.heap` is not empty before the while loop.
            // Therefore, when reach here, data in `self.heap` is all drained into `self.in_progress_rows`.
            debug_assert!(!self.in_progess_rows.is_empty());
            self.state = ProcessorState::Output;
            break;
        }
    }
}

Processor 状态机

由于 Databend 的流水线框架基于 Morsel-Driven Parallelism 的，所以需要为每一个 Processor 算子设计一个状态机。这里简单描述一下 MultiMergeSort 的状态机模型。整体状态机大致如下图所示，其中省略了一些边界情况。

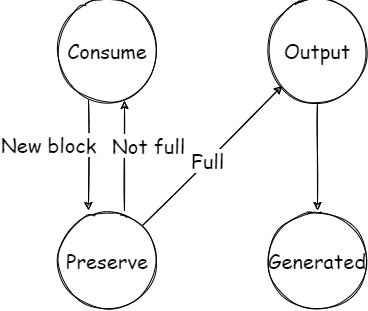
• Consume: 拉取数据 block，转为 Preserve 状态。
• Preserve: 核心逻辑状态。将 block 推入堆中并执行上一节所示的堆操作流程。若可以进行输出，则转为 Output 状态；否则回到 Consume 状态进行下一波数据拉取。
• Output: 构造输出 block，转为 Generated 状态。
• Generated: 将需要输出的 block 推入 output port。

性能分析

上图是流化 MergeSort 之后（没有进行堆操作优化）的火焰图。可见，性能瓶颈从归并排序转换了堆操作，其中推操作的瓶颈又在于 Cursor 之间的比较运算。所以接下来便引出了本次的第二个优化点：Row Format。

优化二：Row Format

在堆操作中需要对不同行的排序键进行比较运算。Databend 基于 arrow2 来做的内存列式存储与计算，在比较两列中某一行数据时，需要先调用 build_compare 为两列建立比较函数，然后再调用比较函数得到两列中指定两行的比较结果。由于 build_compare 所得到的函数会根据待比较两列的类型进行动态分发（虚函数），并且需要在堆内存进行随机寻址，所以效率十分低下（从上面的火焰图也可以看出）。

因此，我们想要消除 build_comapre 以及列内随机查询带来的开销。如果 Cursor 可以直接相比，而不是会间接进行一层函数调用就好了——这就是内存 Row 结构产生的契机。除了排序计算，Row 结构在 Join 运算中也会带来性能上的提升，不过这是后话了。

这里的需求就是：将列数据转换为一种可以直接用来比较的行数据。正好前不久，Apache Arrow 引入了一种专门用于比较运算的 Row Format，并将其用在了 arrow-datafusion 并为排序带来了 50% ~ 70% 的性能提升，于是我便将其移植到了 arrow2 中以供 Databend 使用。

实现细节

整体的实现细节可参见 arrow 的博客。我在这里进行一些重要类型的说明。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

┌─────┐   ┌─────┐   ┌─────┐
│     │   │     │   │     │
├─────┤ ┌ ┼─────┼ ─ ┼─────┼ ┐              ┏━━━━━━━━━━━━━┓
│     │   │     │   │     │  ─────────────▶┃             ┃
├─────┤ └ ┼─────┼ ─ ┼─────┼ ┘              ┗━━━━━━━━━━━━━┛
│     │   │     │   │     │
└─────┘   └─────┘   └─────┘
            ...
┌─────┐ ┌ ┬─────┬ ─ ┬─────┬ ┐              ┏━━━━━━━━┓
│     │   │     │   │     │  ─────────────▶┃        ┃
└─────┘ └ ┴─────┴ ─ ┴─────┴ ┘              ┗━━━━━━━━┛
Customer    State    Orders
 UInt64      Utf8     F64

       Input Arrays                          Row Format
        (Columns)

通用逻辑

• 整个行数据编码由各个排序键编码依次连接而成。

• 所有类型的数据的第一个字节都是用来表示是否为 NULL。若为 NULL，只占一个字节。

  • 若不为 NULL，此字节为 0x01（一般情况，变长类型可能为 0x02）。
  • 若排序选项 null first 为 true，NULL 字节为 0x00。
  • 若排序选项 null first 为 false，NULL 字节为 0xFF。

• 如果排序选项为降序排序，则将整个数据按位反转。

• 行的比较即为底层二进制数据的 memcmp 比较，即：依次比较二进制位，碰到第一个不同二进制数是便可得出结果。

无符号整数

按照大端方式编码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

             ┌──┬──┬──┬──┐      ┌──┬──┬──┬──┬──┐
  3          │03│00│00│00│      │01│00│00│00│03│
             └──┴──┴──┴──┘      └──┴──┴──┴──┴──┘
             ┌──┬──┬──┬──┐      ┌──┬──┬──┬──┬──┐
 258         │02│01│00│00│      │01│00│00│01│02│
             └──┴──┴──┴──┘      └──┴──┴──┴──┴──┘
             ┌──┬──┬──┬──┐      ┌──┬──┬──┬──┬──┐
23423        │7F│5B│00│00│      │01│00│00│5B│7F│
             └──┴──┴──┴──┘      └──┴──┴──┴──┴──┘
             ┌──┬──┬──┬──┐      ┌──┬──┬──┬──┬──┐
NULL         │??│??│??│??│      │00│00│00│00│00│
             └──┴──┴──┴──┘      └──┴──┴──┴──┴──┘

            32-bit (4 bytes)        Row Format
Value        Little Endian

有符号整数

按照补码编码。

1
2
3
4
5
6
7
8
9

      ┌──┬──┬──┬──┐       ┌──┬──┬──┬──┐       ┌──┬──┬──┬──┬──┐
   5  │05│00│00│00│       │05│00│00│80│       │01│80│00│00│05│
      └──┴──┴──┴──┘       └──┴──┴──┴──┘       └──┴──┴──┴──┴──┘
      ┌──┬──┬──┬──┐       ┌──┬──┬──┬──┐       ┌──┬──┬──┬──┬──┐
  -5  │FB│FF│FF│FF│       │FB│FF│FF│7F│       │01│7F│FF│FF│FB│
      └──┴──┴──┴──┘       └──┴──┴──┴──┘       └──┴──┴──┴──┴──┘

Value  32-bit (4 bytes)    High bit flipped      Row Format
        Little Endian

浮点数

按照 IEEE 754。

变长类型（字符串，字符数组）

基本思想：COBS 编码。

NULL 用 0x00 表示，空串用 0x01 表示，非空串用 0x02 打头（使得非空串一定比空串大）。变长类型的数据长度被设计为 32 的整数倍，即：未满 32 字节用 0 填充到 32字节（选择 32 是因为 AVX-256 一次可拷贝 32 字节）。每 32 字节最后用 0xFF 结束，除了最后一块，最后一块用该块的数据长度来结束。下面用 4 字节代替 32 字节来演示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

                      ┌───┬───┬───┬───┬───┬───┐
 "MEEP"               │02 │'M'│'E'│'E'│'P'│04 │
                      └───┴───┴───┴───┴───┴───┘

                      ┌───┐
 ""                   │01 |
                      └───┘

 NULL                 ┌───┐
                      │00 │
                      └───┘

"Defenestration"      ┌───┬───┬───┬───┬───┬───┐
                      │02 │'D'│'e'│'f'│'e'│FF │
                      └───┼───┼───┼───┼───┼───┤
                          │'n'│'e'│'s'│'t'│FF │
                          ├───┼───┼───┼───┼───┤
                          │'r'│'a'│'t'│'r'│FF │
                          ├───┼───┼───┼───┼───┤
                          │'a'│'t'│'i'│'o'│FF │
                          ├───┼───┼───┼───┼───┤
                          │'n'│00 │00 │00 │ 1 │
                          └───┴───┴───┴───┴───┘

分块这种设计让变长类型转换为了定长类型，能够解决有多个排序键时可能引入的问题。如果直接按照变长类型本身进行编码，考虑下面这一种场景，其中有两个排序键都为变长类型，且他们的编码都如下：

1
2
3
4
5

┌───┬───┬───┬───┬───┬───┐
│02 │ 01│ 02│ 02│ 01│ 01│
└───┴───┴───┴───┴───┴───┘
ckey 1: 02 01, 02 02 01 01
ckey 2: 02 01 02, 02 01 01

由于 ckey1 的第一个 key 比 ckey2 的第一个 key 小，最后的结果应该是 ckey1 < ckey2，然而按照这种 encoding 方式结果却是相等！只要不按照定长划分，当存在多个排序键时都可能存在问题。

而上述分块的编码方式一定可以在当前排序键的范围内得出比较结果（显而易见）。

字典类型

字典类型是 Arrow 中一种用来保存低基数数据的类型，在 Databend 中似乎没有使用，这里不做过多介绍。想了解的话请到博客原文中查看。

性能分析

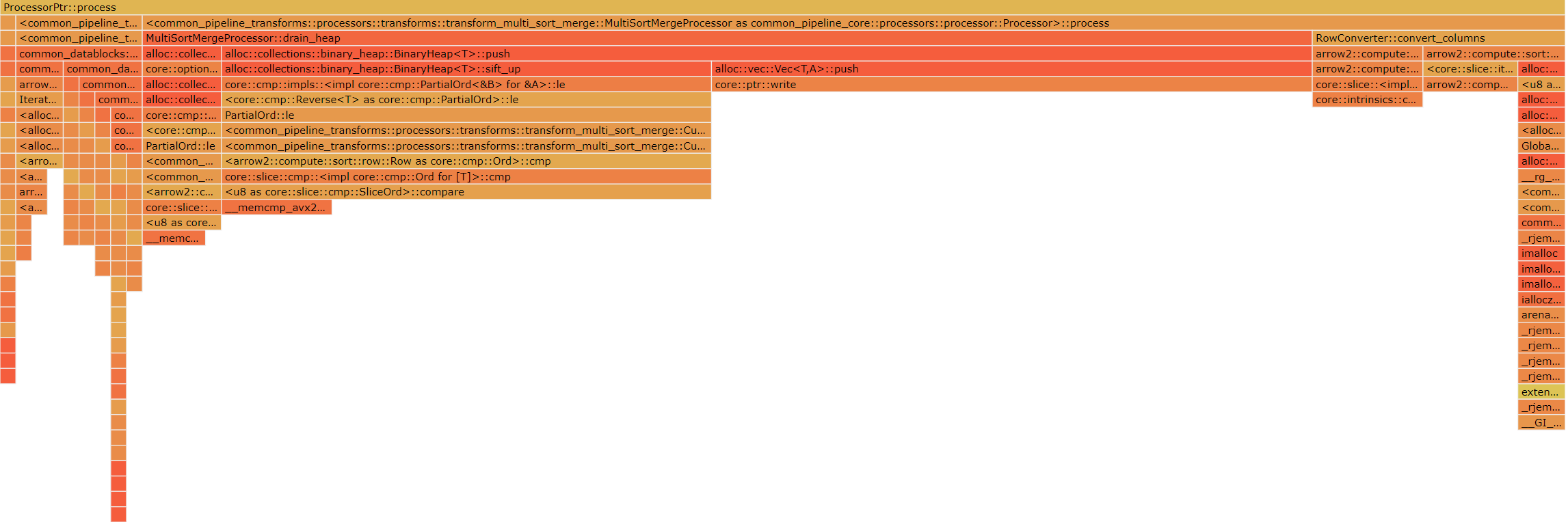
和上一节的火焰图相比，可以看出，比较操作的占比大幅度减小，比较还用上了 avx2 向量化指令集进行 memcmp 的比较。

最终优化结果

可见，经过以上的优化，使得排序运算得到了不小的提升。

另外，对 hits 表（1亿行数据） 的 RECLUSTER 操作也不会 OOM 了（内存维持在 10G 以内）。

其他优化点

1. 并行二路归并排序

DuckDB 使用这种方法来优化二路归并排序。并行二路归并排序的实现来源于论文 Merge Path - A Visually Intuitive Approach to Parallel Merging，其基本思想是将找到两个有序序列中的排序交叉点，将两个序列按照交叉点分组，使得每个组内的两个数据部分独自归并排序，最后将所有块的结果合并。序列的分组使得每个组的归并排序可以并行执行，不会互相影响，最后直接这便可得到全序结果。

DuckDB 排序优化博客：https://duckdb.org/2021/08/27/external-sorting.html。

2. 基数排序

DuckDB 与 ClickHouse 等数据库都引入了基数排序。基数排序是一种非比较的基于分布的排序方式，时间复杂度为 O(nk)，其中 k 是排序键的宽度（比如 Int32 的宽度是 4 字节），n 是排序键个数。当 n 很大的时候，基数排序的性能优势就会显现出来。

3. 特化 Cursor

如果排序键只有一个，且是 non-nullable 的简单类型，便可以将 Rows 直接 downcast 为简单类型的一维数组，对于简单类型有着非常好的优化效果。类似的，如果存在多个排序键，但是他们可以合并成一个简单的排序键（比如两个 i32 可以合并为 i64）。这是一类大的优化方向。

局限性

如果排序键为聚合函数的结果，以目前的实现来说，用于排序的始终就只有一条流水线，无法进行流化多路归并。需要针对这种情况优化流水线。

1

SELECT COUNT(*) as c FROM table ORDER BY c;